Whether you work on large-scale data analysis, are interested in geospatial modeling or want to solve linear equations in your deep learning applications, you’ll sooner or later come across the NumPy library for numerical computing.
This powerful framework lets you process your tabular data at a high speed. But what is a NumPy array, and how can you make the most of it?
What is NumPy?
NumPy is a Python library for numerical computing (the name stands for Numerical Python). It’s optimized for speed and used in many Python libraries (such as pandas or SciPy) that require fast and accurate computation of large data collections. You can easily install NumPy using pip:

In a Python shell, you’d normally import NumPy by using an alias:

A quick tip: Importing NumPy with the np alias saves us time and space whenever we want to use the library’s functionalities.
What is Numerical Computation?
Numerical computation is used to create algorithms that approximate complex mathematical functions through an iterative process. When we operate with complex data frames, we use linear algebra and calculus to find the right solutions. Numerical computation seeks to break these down into simpler equations.
What is a NumPy Array?
We previously mentioned “data frames” and “tabular data.” Both terms refer to a grid-like data type used to represent numeric values in a structured way. In mathematics, we call these structures “vectors” (when they’re one-dimensional) or “matrices” (when multidimensional). NumPy represents them with a single data type: the NumPy array.
There are various way of creating a NumPy arrays, the simplest of which is by converting a Python list:

Note that while we commonly call this data type a NumPy array, the official name is numpy.ndarray (for N-dimensional array), which is tougher to pronounce:

What are the dimensions of our array?

As we can see, ndim really only prints the number of dimensions. The shape method gives us a little bit more information about our Fibonacci sequence:

This tuple tells us two things: Our array is one-dimensional (since we only see one value), and it holds 6 values. How about a two-dimensional array? We once again initialize it from a Python list, but this time we use a nested list to let NumPy know that it’s dealing with a two-dimensional array (or a table, as we would normally call it).
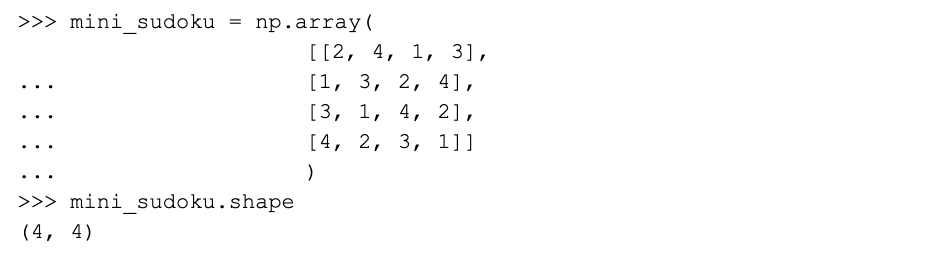
To get an array’s value at a certain position, we may index it with the normal Python syntax, using square brackets. Suppose we want to get the value of the second entry in the first row (recall that Python starts counting from zero). We always give the row value first:

The second value in the first row of our small Sudoku array is 4. Comma-separating the indices returns the same result:

Why Use NumPy Arrays Instead of Nested Lists?
In the example above, we could have achieved the same result by indexing a Python nested list, even without transforming it into a NumPy array:
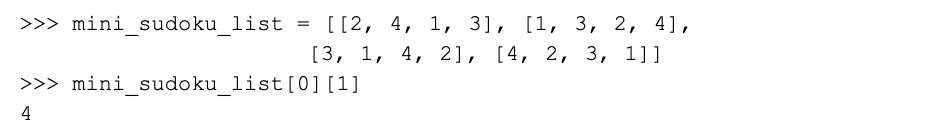
So why would we go these lengths to use NumPy to process our arrays? There are many arguments as to why, all of which boil down to these two performance benefits: Compared to plain Python, NumPy is a) faster for the computer and b) also faster for the programmer.
Faster for the Computer
When you deal with high-dimensional data frames with millions of data points, you find that the processing speed varies greatly with the framework. To optimize performance, NumPy was written in C — a powerful lower-level programming language. Python itself was also written in C and allows for C extensions.
While a Python list is implemented as a collection of pointers to different memory locations, C stores arrays in contiguous memory. This means that we can much more easily access the elements of a C-style data frame! Whenever we create an array in C (or in NumPy), the NumPy extension code reserves space in memory to ensure that it can store the data contiguously.
Faster for the Programmer
Of course, faster computation of large arrays saves the programmer time, too. Likewise, NumPy saves us coding time by offering a range of useful functions for matrix operations. Suppose for instance that you want to take the transpose of a matrix. You would have to write a nested for-loop to achieve that in Python. But in NumPy here’s all it would take:

Pretty elegant, isn’t it? In the next section, we’ll show you a few more cool things you can do with NumPy arrays — from matrix arithmetics to creating large arrays from scratch.
What are Some Useful NumPy Array Operations?
Matrix Arithmetics
Imagine your friend Claire moved to a remote island and wants to convince you to join her by sending you a list of the past six months’ average temperatures. Alas, your friend uses Fahrenheit and you only understand Celsius! We can easily convert her values to something we understand using NumPy.

Looks like we should start packing our bags… Note that this type of operation is not as easily performed in plain Python. When you try to do the same two operations on a list in Python, you’ll get an error. That’s because NumPy implicitly uses broadcasting, meaning it internally converts our scalar values to arrays. Let’s look at a few more useful NumPy array operations.
Array Generation
Aside from the methods that we’ve seen above, there are a few more functions for generating NumPy arrays. np.ones generates a matrix full of 1s. Just pass the shape of the matrix you want to the function:

Similarly, np.zeros produces an array full of 0s:

And if you want to fill your array with another number, use np.full. The first argument is again the shape of the array; the second is the value that you want to fill it with.

On occasion you’ll need to work with large matrices, but won’t care about the exact values inside the cells (e.g. when you want to try out your code with toy data). In such cases, np.random comes to your help. You can generate an array with random integers from a certain range of numbers, or you can fill the cell of your matrix with floating point numbers.

In the first example, we told NumPy to generate a matrix with two rows and three columns filled with integers between 0 and 100. In the second, NumPy created an array with the identical dimensions, this time sampling from a uniform distribution between 0 and 1.
Learn More
We trust you were able to pick up a thing or two about NumPy arrays. But there’s much more for you to learn as a Python programmer.
Check out our Introduction to Programming Nanodegree to prepare yourself for work in exciting fields like Web and App Development, Machine Learning, Data Science and AI.