Lesson 1
Intro to Algorithms
Course
This class will give you an introduction to the design and analysis of algorithms, enabling you to analyze networks and discover how individuals are connected.
This class will give you an introduction to the design and analysis of algorithms, enabling you to analyze networks and discover how individuals are connected.
Last Updated September 10, 2023
No experience required
Course Lessons
Lesson 2
Problem Set 1
Lesson 3
Growth Rates in Social Networks
Lesson 4
Problem Set 2
Lesson 5
Problem Set 2 Solutions
Lesson 6
Basic Graph Algorithms
Lesson 7
Problem Set 3
Lesson 8
Problem Set 3 Solutions
Lesson 9
It's Who You Know
Lesson 10
Problem Set 4
Lesson 11
Problem Set 4 Solutions
Lesson 12
Strong and Weak Bonds
Lesson 13
Problem Set 5
Lesson 14
Hardness of Network Problems
Lesson 15
Problem Set 6
Lesson 16
Lesson 7
Lesson 17
Final Assessment
Lesson 18
Extra Challenge Problems
Taught By The Best

Michael Littman
Instructor
The Udacity Difference
Combine technology training for employees with industry experts, mentors, and projects, for critical thinking that pushes innovation. Our proven upskilling system goes after success—relentlessly.

Demonstrate proficiency with practical projects
Projects are based on real-world scenarios and challenges, allowing you to apply the skills you learn to practical situations, while giving you real hands-on experience.
Gain proven experience
Retain knowledge longer
Apply new skills immediately
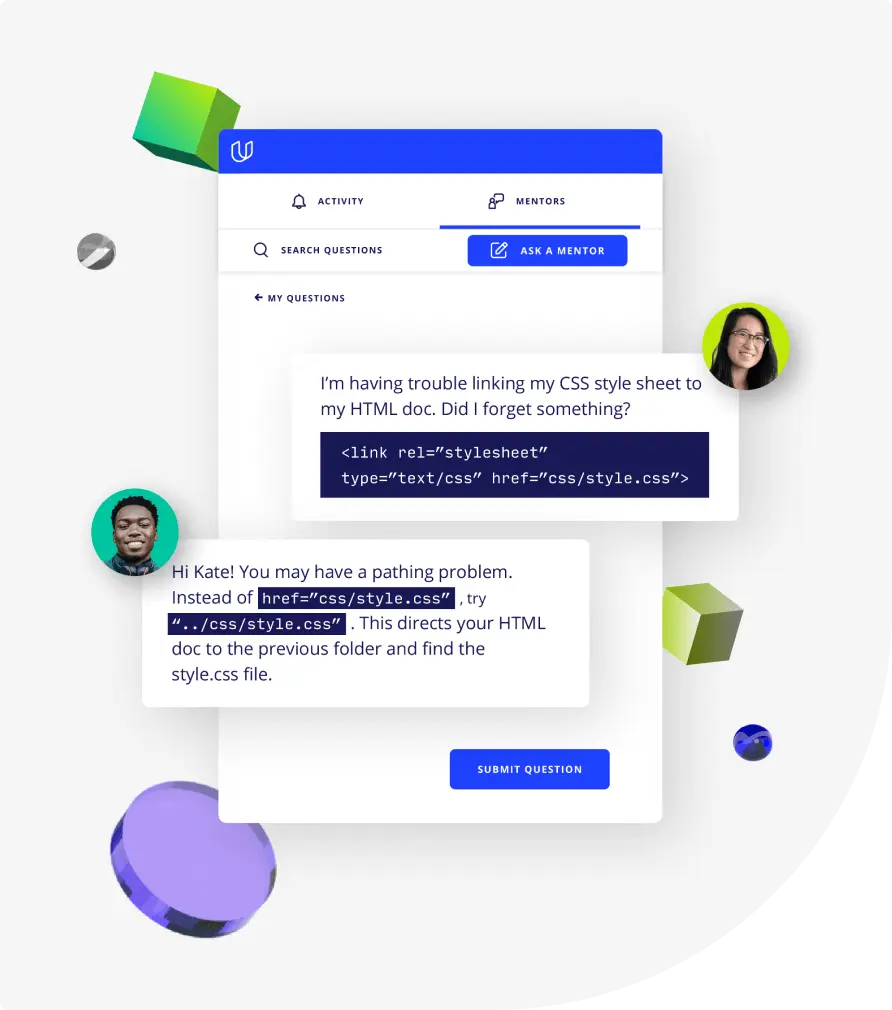
Top-tier services to ensure learner success
Reviewers provide timely and constructive feedback on your project submissions, highlighting areas of improvement and offering practical tips to enhance your work.
Get help from subject matter experts
Learn industry best practices
Gain valuable insights and improve your skills